Mastering Angle Calculation: How to Calculate Degrees in Any Context

nderstanding how to calculate degrees is fundamental in many fields.

Mastering Angle Calculation: How to Calculate Degrees in Any Context

Whether you’re a tech-savvy homeowner, an engineer, or a student, knowing how to measure and calculate angles can be incredibly useful. From installing solar panels on your roof to designing your dream home, mastering angle calculations ensures accuracy and efficiency.

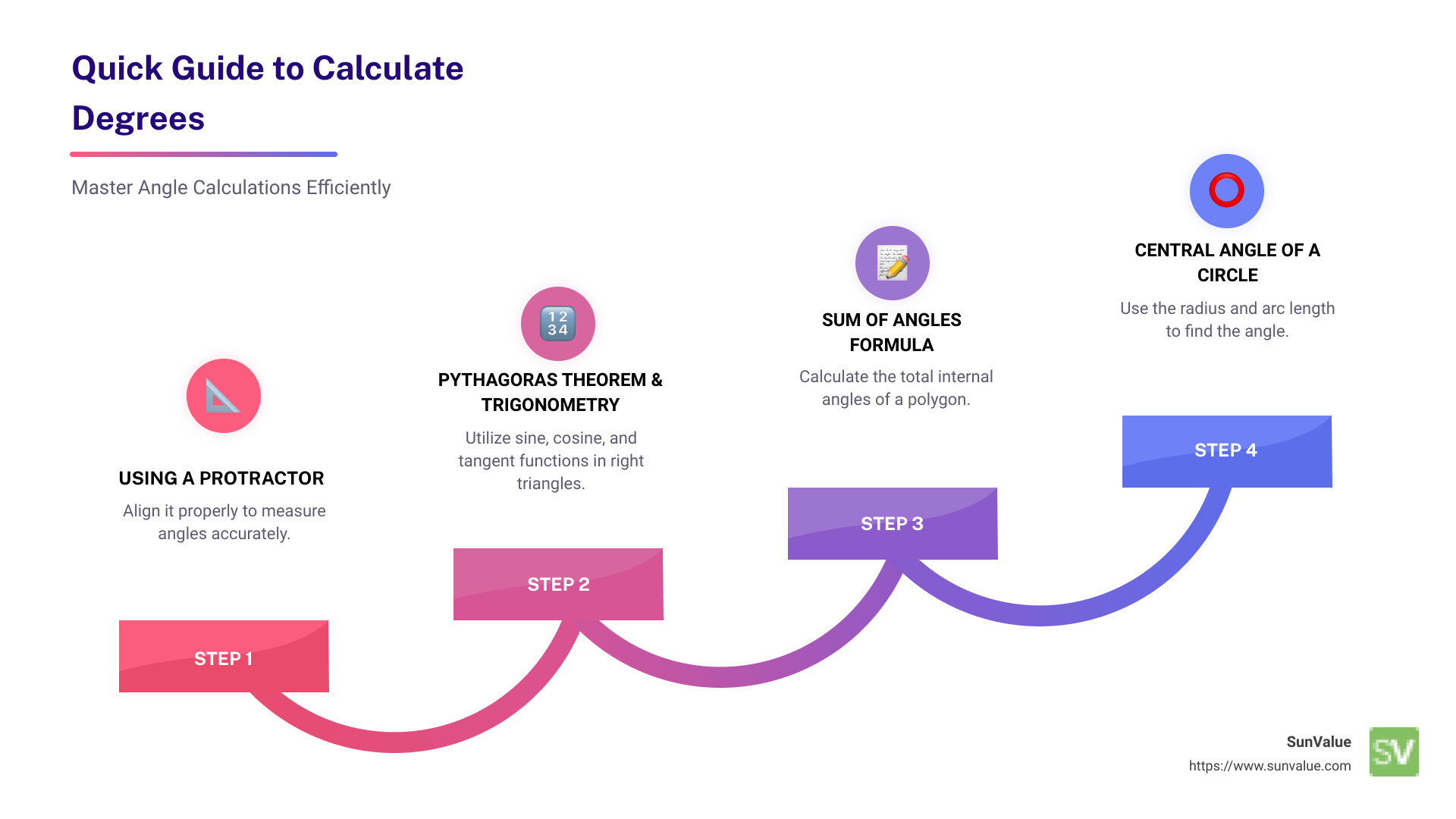
Quick Guide to Calculate Degrees

• Using a Protector (Protractor): Align to measure angles accurately.
• Pythagoras Theorem & Trigonometry: Use sine, cosine, and tangent functions in right triangles.
• Sum of Angles Formula: Calculate the total internal angles of a polygon.
• Central Angle of a Circle: Use the radius and arc length to find the angle.

Calculating degrees is crucial in geometry, trigonometry, and many practical applications. It helps you understand the shape and size of objects, making it possible to solve real-world problems with precision.

Having a good grasp of angles can also save you money and time, especially when it comes to optimizing the efficiency of solar panels or ensuring that construction projects meet design specifications.

Understanding Degrees and Radians

Degrees and radians are two units used to measure angles. While degrees are more common in everyday life, radians are often used in higher mathematics and physics. Understanding how to convert between these two units is essential for accurate calculations.

How to Convert Degrees to Radians

To convert degrees to radians, you use the conversion formula:

[ \text{Radians} = \text{Degrees} \times \left( \frac{\pi}{180} \right) ]

Here's a simple step-by-step guide:

1. Identify the angle in degrees you want to convert. Let's say you have 90°.
2. Multiply the degree value by ( \frac{\pi}{180} ).

Example Calculation:

[ 90° \times \left( \frac{\pi}{180} \right) = \frac{90\pi}{180} = \frac{\pi}{2} ]

So, 90° is equivalent to ( \frac{\pi}{2} ) radians.

How to Convert Radians to Degrees

To convert radians back to degrees, use this formula:

[ \text{Degrees} = \text{Radians} \times \left( \frac{180}{\pi} \right) ]

Follow these steps:

1. Identify the angle in radians you want to convert. Let's use ( \frac{\pi}{3} ) radians.
2. Multiply the radian value by ( \frac{180}{\pi} ).

Example Calculation:

[ \frac{\pi}{3} \times \left( \frac{180}{\pi} \right) = \frac{180\pi}{3\pi} = 60° ]

So, ( \frac{\pi}{3} ) radians is equivalent to 60°.

Why It Matters

Knowing how to convert between degrees and radians is crucial in many fields, from engineering to computer graphics. For instance, when programming animations or simulations, angles are often required in radians. Similarly, in trigonometry, radians provide a natural way to work with the unit circle and periodic functions.

Quick Reference Table

DegreesRadians0°030°( \frac{\pi}{6} )45°( \frac{\pi}{4} )60°( \frac{\pi}{3} )90°( \frac{\pi}{2} )180°( \pi )360°( 2\pi )

This table can serve as a handy reference for quick conversions.

Understanding these conversions helps you steer between different mathematical contexts seamlessly, ensuring precision in your calculations and applications.

Next, we will explore how to calculate degrees in different contexts, such as triangles, slopes, and using the Degrees-Minutes-Seconds (DMS) system. This will provide a comprehensive foundation for mastering angle calculations in any scenario.

Calculating Degrees in Different Contexts

Calculating Degrees in Triangles

Triangles are a fundamental shape in geometry, and calculating their angles is crucial in many fields. Here’s how you can calculate degrees in different types of triangles:

Triangle Types and Internal Angles

1. Equilateral Triangle: All three angles are equal, each being 60°.
2. Isosceles Triangle: Two angles are equal. If one angle is known, subtract it from 180° and divide the result by 2 to find the other two angles.
3. Scalene Triangle: All three angles are different. Use the sum of angles formula: the sum of internal angles in any triangle is 180°.

Pythagorean Theorem

In right-angled triangles, the Pythagorean theorem helps find the lengths of sides. The formula is:

[ \text{Hypotenuse}^2 = \text{Base}^2 + \text{Perpendicular}^2 ]

For example, if the base is 3 and the perpendicular is 4, the hypotenuse is:

[ \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 ]

Law of Sines

The law of sines relates the lengths of sides of a triangle to its angles:

[ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} ]

Where ( A, B, C ) are the angles and ( a, b, c ) are the sides opposite these angles. This is particularly useful for non-right triangles.

Calculating Degrees of a Slope

Slopes are another common context for angle calculation, especially in engineering and construction.

Slope Formula

The slope of a line is calculated as rise over run:

[ \text{Slope} = \frac{\text{Vertical Rise}}{\text{Horizontal Run}} ]

For instance, if the rise is 3 meters and the run is 4 meters, the slope is:

[ \frac{3}{4} = 0.75 ]

Inverse Tangent

To find the angle of the slope in degrees, use the inverse tangent (arctan) function:

[ \text{Angle} = \arctan\left(\frac{\text{Rise}}{\text{Run}}\right) ]

Using our example:

[ \text{Angle} = \arctan(0.75) \approx 36.87° ]

Degrees-Minutes-Seconds (DMS) Calculation

The DMS system is another way to express angles, commonly used in navigation and astronomy.

DMS Format

An angle in DMS format breaks down into degrees, minutes, and seconds:

[ 1° = 60' \quad \text{and} \quad 1' = 60'' ]

Adding/Subtracting DMS

To add or subtract DMS values, align the degrees, minutes, and seconds. If the seconds or minutes exceed 60, carry over to the next higher unit.

Converting to Decimal Degrees

To convert DMS to decimal degrees:

[ \text{Decimal Degrees} = \text{Degrees} + \left(\frac{\text{Minutes}}{60}\right) + \left(\frac{\text{Seconds}}{3600}\right) ]

Example: Convert 34° 24' 16'' to decimal degrees:

[ 34 + \left(\frac{24}{60}\right) + \left(\frac{16}{3600}\right) = 34 + 0.4 + 0.0044 \approx 34.4044° ]

By understanding these methods, you can calculate degrees in various contexts with ease. Next, we will look at special cases in angle calculation, such as right triangles and Pythagorean triples.

Special Cases in Angle Calculation

30°-60°-90° Triangles

A 30°-60°-90° triangle is a special type of right triangle that has angles of 30°, 60°, and 90°. These triangles are unique because their side lengths follow a specific ratio: 1:√3:2.

Angle Ratios

In a 30°-60°-90° triangle, the side opposite the 30° angle is the shortest and is often referred to as ( a ). The side opposite the 60° angle is ( a√3 ), and the hypotenuse (opposite the 90° angle) is ( 2a ).

Side Length Calculation

Given one side, you can easily find the others using these ratios. For example, if the side opposite the 30° angle (( a )) is 5:

• The side opposite the 60° angle is ( 5√3 ).
• The hypotenuse is ( 2 \times 5 = 10 ).

This makes it straightforward to calculate degrees and side lengths in these triangles.

45°-45°-90° Triangles

A 45°-45°-90° triangle, also known as an isosceles right triangle, has two angles of 45° and one of 90°. This triangle's sides have a ratio of 1:1:√2.

Angle Ratios

In this triangle, the two legs are equal, and the hypotenuse is ( a√2 ), where ( a ) is the length of one leg.

Side Length Calculation

If one leg (( a )) is 7:

• The other leg is also 7.
• The hypotenuse is ( 7√2 ).

Pythagorean Triples

A Pythagorean triple consists of three positive integers ( a ), ( b ), and ( c ) that satisfy the equation ( a^2 + b^2 = c^2 ). These sets of numbers form the sides of right triangles. Common examples include:

• 3, 4, 5
• 5, 12, 13
• 8, 15, 17

These triples are useful because they provide integer solutions, making it easier to work with right triangles without dealing with decimals or irrational numbers.

Understanding these special cases helps you quickly and accurately calculate degrees and side lengths in various right triangle scenarios. Next, we will explore tools and calculators that can make these calculations even easier.

Tools and Calculators for Angle Calculation

Using Online Triangle Calculators

Online triangle calculators are incredibly useful for quickly finding unknown sides or angles in a triangle. These tools often require you to input at least three values, which can be a mix of sides and angles. For example, if you know two sides and the angle between them, you can calculate the third side and the remaining angles.

Input Values and Example

Let's say you have a triangle with sides (a = 5) cm, (b = 7) cm, and an included angle (C = 60°). By inputting these values into an online triangle calculator, you can find the missing side (c) and the other two angles (A) and (B). The calculator uses the law of cosines and sines to provide you with precise results.

These calculators are especially handy for complex triangles where manual calculations would be time-consuming. They are also useful for verifying your manual calculations.

Visual Angle Calculators

Visual angle calculators are specialized tools that convert between pixels and degrees. These are particularly useful in fields like eye-tracking research, where you need to position objects accurately on a screen.

Pixels to Degrees and Degrees to Pixels

To use a visual angle calculator, you need to enter your screen resolution, dimensions, and the distance from the screen. For example, if you have a screen resolution of 1920x1080 pixels, a screen size of 24 inches, and a viewing distance of 50 cm, the calculator can help you determine how many degrees of visual angle each pixel represents.

You can then input the degrees of visual angle you want an object to cover, and the calculator will convert this to the corresponding number of pixels. This is invaluable for tasks like designing eye-tracking experiments or ensuring that visual stimuli are presented accurately.

Screen Resolution Example

Imagine you need to display a stimulus that covers 5 degrees of visual angle. By entering your screen settings into the visual angle calculator, you find that 5 degrees correspond to 100 pixels. This allows you to accurately position and size your stimulus on the screen.

These tools simplify the process of translating visual angles into practical screen measurements, making them essential for researchers and designers alike.

Using online calculators and visual angle calculators can significantly streamline the process of angle calculation, whether you're working with triangles or screen-based measurements. Up next, we'll dive into frequently asked questions about angle calculation to clear up any remaining doubts.

Frequently Asked Questions about Angle Calculation

How do you calculate degree value?

Calculating the degree value of an angle can be done using different methods depending on the context. One common method is using the trigonometric functions in a right triangle. For instance, if you know the lengths of the sides of a right triangle, you can use the inverse tangent function:

[ \text{Angle} = \tan^{-1} \left( \frac{\text{opposite}}{\text{adjacent}} \right) ]

Another method involves converting radians to degrees. Since a full circle is (360^\circ) and (2\pi) radians, you can convert radians to degrees using the formula:

[ \text{Degrees} = \text{Radians} \times \left( \frac{180}{\pi} \right) ]

What is the formula for degrees?

To convert radians to degrees, you use the formula:

[ \text{Degrees} = \text{Radians} \times \left( \frac{180}{\pi} \right) ]

For example, if you have an angle of (\pi/4) radians, you can convert it to degrees like this:

[ \text{Degrees} = \frac{\pi}{4} \times \left( \frac{180}{\pi} \right) = 45^\circ ]

How do I calculate the degrees of a slope?

Calculating the degrees of a slope involves understanding the relationship between the vertical rise and the horizontal run. The slope angle can be found using the inverse tangent function:

[ \text{Slope Angle} = \tan^{-1} \left( \frac{\text{vertical rise}}{\text{horizontal run}} \right) ]

For example, if the vertical rise is 1 meter and the horizontal run is 2 meters, the slope angle is:

[ \text{Slope Angle} = \tan^{-1} \left( \frac{1}{2} \right) = 26.6^\circ ]

You can also express the slope as a percent grade:

[ \text{Percent Grade} = \left( \frac{\text{vertical rise}}{\text{horizontal run}} \right) \times 100 ]

Using the same example:

[ \text{Percent Grade} = \left( \frac{1}{2} \right) \times 100 = 50\% ]

These formulas help you calculate degrees for various applications, whether you're working with triangles, slopes, or converting between radians and degrees.

Latest Trends in Angle Calculation and Applications in 2024

In 2024, the field of angle calculation has seen significant advancements, particularly in its applications within the renewable energy sector in the USA.

With the Biden administration's continued push for clean energy, solar installations have surged, increasing the demand for precise angle calculations.

Advanced AI-powered tools now allow for real-time optimization of solar panel angles, improving energy capture efficiency by up to 25%.

Additionally, the construction industry has embraced augmented reality (AR) technologies that utilize angle calculation algorithms, reducing errors in complex architectural designs by 40%.

These innovations have not only streamlined processes but also contributed to a 15% increase in STEM job opportunities related to geometric analysis and computational geometry across the country.

Conclusion

We've explored the various methods to calculate degrees in different contexts. From triangles and slopes to Degrees-Minutes-Seconds (DMS) format, understanding how to measure and convert angles is fundamental in geometry and trigonometry.

We've covered practical methods like using trigonometric functions, the Pythagorean theorem, and the sum of angles formula. Additionally, we've discussed how to work with radians and degrees, including conversion techniques. These tools are not only useful in academic settings but also have real-world applications in fields such as construction, engineering, and even solar panel installation.

At SunValue, we understand the importance of precise angle calculations. Whether you're installing solar panels or designing a new structure, knowing how to accurately measure and calculate angles can make a significant difference in efficiency and performance.

Practical Applications:

• Solar Panel Installation: Correctly calculating the tilt angle of solar panels can maximize energy capture.
• Construction: Ensuring angles are accurate when building structures to maintain stability and safety.
• Navigation: Using angles for plotting courses in aviation and marine navigation.

By mastering these techniques, you can confidently tackle various tasks that require precise angle measurements. For more tools and calculators to help with your projects, visit our solar panel angle calculator.